Мислення в дії - рішення задач (ВВП)
Книга «Вступ у психологію». Автори - Р. Л. Аткінсон, Р. С. Аткінсон, Е. Е. Сміт, Д. Дж. Бем, С. Нолен-Хоэксема.
Стаття з розділ 9. Мислення і мова
Для багатьох людей рішення завдань уособлює саме мислення. При вирішенні завдань ми прагнемо до мети, не маючи готового засоби для її досягнення. Ми повинні розбити мета на підцілі і, можливо, поділити ці підцілі далі, на ще менші підцілі, поки не дійдемо до рівня, на якому ми маємо в своєму розпорядженні необхідними засобами (Anderson, 1990).
Ці моменти можна проілюструвати на прикладі простої задачі. Припустимо, вам треба розгадати незнайому комбінацію цифрового замка. Ви знаєте тільки те, що в цій комбінації 4 цифри і що, як тільки ви набираєте вірну цифру, ви чуєте клацання. Загальна мета - знайти комбінацію. Замість того, щоб пробувати 4 цифри в довільному порядку, більшість людей поділяють спільну мету на 4 підцілі, кожна з яких відповідає знаходженню одній з 4 цифр комбінації. Перша подцель - знайти першу цифру, і у вас є спосіб її досягнення, а саме: повертати замок повільно, поки не почуєте клацання. Друга подцель - знайти другу цифру, і для цього можна використовувати ту ж саму процедуру, і так далі з усіма залишаються подцелями.
Стратегії розподілу мети на підцілі - це головне питання у вивченні вирішення завдань. Інше питання в тому, як люди подумки уявляють собі завдання, оскільки від цього теж залежить легкість вирішення завдання. Обидва ці питання розглядаються нижче.
Стратегії вирішення завдань
Багато чого з того, що ми знаємо про стратегії підрозділу цілей, сходить до досліджень Ньюелла і Саймона (див. напр.: Newell & Simon, 1972). Як правило, ці дослідники просили випробовуваних думати вголос " в процесі рішення важкої задачі; вони аналізували вербальні реакції випробовуваних на ключову для даної стратегії інформацію. Ними був виявлений ряд стратегій загального призначення.
Одна стратегія полягає в скороченні розриву між поточним станом проблемної ситуації і її цільовим станом, в якому досягається рішення. Розглянемо знову завдання з комбінацією цифрового замка. Спочатку наш поточний стан не містить знання ні про одну з цифр, а цільове стан включає знання всіх цифр. Отже, ми встановлюємо подцель, зменшуючи розрив між цими двома станами; визначення першої цифри реалізує цю подцель. Тепер поточний стан включає знання першої цифри. Розрив між поточним станом та цільовим все ще існує, і його можна зменшити, визначивши другу цифру, і т. д. Отже, головна ідея скорочення розриву полягає у встановленні підцілей, досягнення кожної з яких переводить нас у стан, більш близьке до нашої мети.
Подібна, але більш складна стратегія називається «аналіз засобу і результату». В ній поточний стан порівнюється з цільовим станом, щоб знайти найбільш важлива відмінність між' ними; усунення цієї розбіжності стає головною подцелью. Потім ведеться пошук кошти або процедури для досягнення цієї підцілі. Якщо така процедура знайдена, але виявляється, що в поточному стані не дає її застосувати, вводиться нова подцель з усунення цієї перешкоди. Ця стратегія застосовується у багатьох випадках рішення завдань на основі здорового глузду. Ось приклад:
Я хочу відвести свого сина в дитячий сад. Які [найбільш важливі] відмінності між тим, що я маю, і тим, що хочу? Одне з них - відстань. Що [яка процедура] змінює відстань? Мій автомобіль. Мій автомобіль не працює. Що потрібно, щоб він запрацював? Новий акумулятор. Де є новий акумулятор? В автомайстерні.
(Newell & Simon, 1972; цит. за: Anderson, 1990, р. 232).
Аналіз засобу і результату - більш складна стратегія порівняно з скороченням розриву, оскільки він дозволяє зробити дію, навіть якщо воно призводить до тимчасового зменшення схожості між поточним станом та цільовим. У вищенаведеному прикладі автомайстерня може перебувати в протилежному напрямку від дитячого садка. Так що, вирушаючи в майстерню, ви тим самим тимчасово збільшуєте відстань до цілі, і все ж цей крок важливий для вирішення завдання.
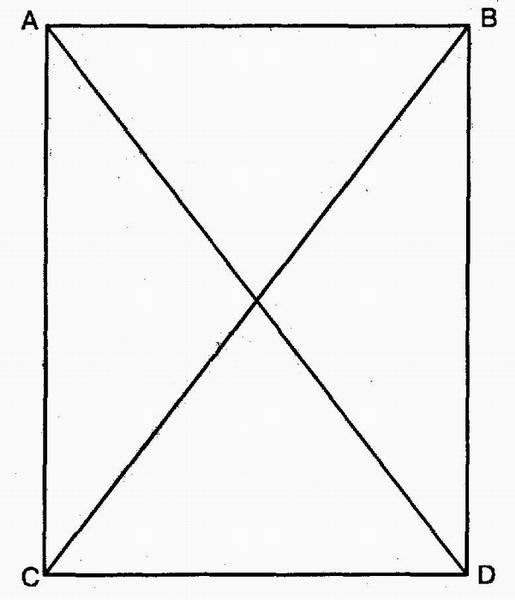
Ще одна стратегія - це дія, в якій відбувається зворотний рух від мети. Вона особливо корисна при вирішенні математичних завдань, приклад однієї з яких показано на рис. 9.12. Задача така: знаючи, що ABCD - прямокутник, довести, що діагоналі AD і ВС дорівнюють. Подумки рухаючись назад, можна міркувати так:
Як довести, що AD і ВС дорівнюють? Я міг би це зробити, якби довів, що трикутники ACD і BDC рівні. Я можу довести, що трикутники ACD і BDC рівні, якщо доведу, що дві сторони до укладений між ними кут рівні.
(взято з: Anderson, 1990, р. 238).
Ми міркуємо, йдучи від мети на підцілі (доводячи рівність трикутників), від цієї підцілі - до іншої підцілі (доводячи, що сторони і кут рівні) і т. д., поки ми не дійдемо до підцілі, для реалізації якої у нас є готовий засіб.
Три розглянуті нами стратегії - скорочення розриву, аналіз засобу і результату і рух від мети - є надзвичайно загальними і можуть застосовуватися практично до будь-якої задачі. Ці стратегії, які часто називають слабкими методами, що не ґрунтуються ні на якому конкретному знанні і можуть бути вродженими. Люди можуть особливо покладатися на ці слабкі методи, коли вони вперше вивчають яку-небудь область і працюють над завданнями з незнайомим змістом. Kale ми незабаром переконаємося, коли люди отримують спеціальні знання в якій-небудь області, вони розробляють більш потужні предметно-орієнтовані методи (і репрезентації), які починають переважати над слабкими методами (Anderson, 1987).
Уявлення про завдання
Здатність вирішити завдання залежить не тільки від стратегії її декомпозиції, але також і від того, як ми її собі уявляємо. Іноді кращим виявляється подання у формі висловлювань (пропозиціональна репрезентація); в інших випадках більш ефективним буде зорове уявлення, або образ. Для ілюстрації розглянемо наступну задачу:
Одного разу вранці, на світанку, чернець став підійматися на гору. Вузький прохід шириною один або два фути спіраллю обвивав гору, ведучи до храму на вершині. Чернець вилазив з різною швидкістю, часто перериваючи шлях для відпочинку. Він дістався до храму незадовго перед заходом сонця. Провівши кілька днів у храмі, і він почав свій шлях назад по тому ж шляху, вийшовши на світанку, і знову йшов з різною швидкістю з багатьма зупинками в дорозі. Його середня швидкість спуску була, звичайно, більше середньої швидкості взбіранія на гору. Доведіть, що на шляху існує певне місце, в якому монах стояв на шляху вперед і назад точно в один і той же час дня (Adams, 1974, р. 4).
Намагаючись вирішити цю задачу, багато людей починають з пропозиційну репрезентації. Вони можуть навіть намагатися виписати ряд рівнянь і незабаром заплутуються. Цю задачу набагато легше вирішити, якщо подавати її візуально. Все, що потрібно зробити, - це уявити подумки, як шлях ченця вгору накладається на його шлях вниз. Уявіть одного ченця, що йде знизу, а іншого - йде зверху. Незалежно від того, яка у них швидкість, в деякий момент часу і в певному місці шляху вони повинні зустрітися. Тому повинно існувати місце на шляху, що чернець займав в обох подорожі у той же самий час дня (зауважте, що в задачі не питається, де знаходиться це місце).
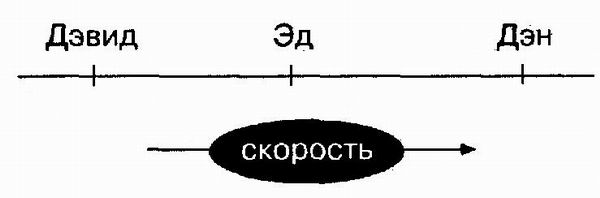
Деякі завдання легко вирішуються шляхом маніпулювання висловлюваннями або образами. Це можна показати на наступному простої задачі: «Ед бігає швидше Девіда, але повільніше Дена; хто з трьох самий повільний? » Щоб розв'язати цю задачу за допомогою висловлювань; зауважимо, що першу частину цього завдання можна представити у вигляді висловлювання, в якому «Девід» - це суб'єкт, а «повільніше, ніж Ед» - предикат. Другу частину, за дачі можна представити у вигляді висловлювання, в якому «Ед» - суб'єкт, а «повільніше Дена» - предикат. Потім можна вивести, що Девід повільніше Дена, звідки випливає, що самий повільний - Девід. Щоб вирішити цю задачу через образи, можна, наприклад, уявити швидкості цих трьох осіб у вигляді трьох точок на лінії:
Потім можна просто вважати відповідь на питання безпосередньо з образу. Очевидно, що деякі люди воліють представляти такі задачі у вигляді висловлювань, а деякі - візуально (Johnson-Laird, 1985).
Крім представлення задачі на мові висловлювань або образів існує питання про те, що представляти. Найчастіше труднощі з завданнями виникають тому, що нам не вдається включити в свою репрезентацію завдання якої-небудь вирішальний фактор, або тому, що ми включили в неї щось, що не є суттєвою частиною завдання. Це можна проілюструвати в експерименті. Одній групі випробовуваних дали завдання закріпити свічку на двері, давши тільки матеріали, показані на рис. 9.13. Рішення полягало в тому, щоб прикріпити коробок до дверей кнопкою і використовувати його як підставку для свічки. Більшості випробовуваних було важко її вирішити, мабуть, тому, що вони уявляли собі коробку як ємність, а не як підставку. Іншій групі піддослідних поставили ту ж задачу, але вийняли вміст коробки. Ці випробовувані успішніше вирішували завдання, мабуть, тому, що вони з меншою ймовірністю включали в свою репрезентацію функцію коробки як ємності і з більшою ймовірністю враховували її функцію як підставки. Дослідження, подібні до цього та інших, розглянутих у даному розділі, дозволяють зрозуміти, чому багато експертів вважають, що хороша репрезентація завдання - це половина успіху на шляху до її вирішення. (Етапи вирішення цього завдання представлені в табл. 9.2.)
Таблиця 9.2. Етапи рішення задачі
- Представити проблему як висловлювання або у візуальній формі.
- Визначити мету.
- Розбити мета на підцілі.
- Вибрати стратегію вирішення задачі і використовувати її для вирішення кожної з підцілей.
Експерти і новачки
У тієї чи іншої предметної області (наприклад, фізики, географії чи шахах) експерти вирішують завдання якісно іншим способом, ніж новачки. Це пояснюється відмінностями у використовуваних ними репрезентациях і стратегіях. У пам'яті експертів може зберігатися більше конкретних репрезентацій, які вони можуть використовувати для рішення задачі. Майстер з шахів, наприклад, може подивитися 5 секунд на складну комбінацію на дошці, включає 20 фігур, і в точності її відтворити; новачок в тій же ситуацій обмежений звичайними 7 ± 2 елементи (див. главу 8). Такий трюк з пам'яттю вдається експертам тому, що з роками практики вони розробили репрезентації багатьох можливих позицій на дошці; ці репрезентації дозволяють їм закодувати складну позицію всього в декількох одиницях. Крім того, ймовірно, саме ці репрезентації лежать в основі їх переваги в шаховій грі. Майстер може зберігати цілих 50 000 конфігурацій і знати, що робити в кожній з них. Отже, майстри шахів можуть, по суті, «бачити» можливі ходи; їм не треба вигадувати, як роблять новачки (Chase & Simon, 1973; Simon & Gilmartin, 1973).
Навіть зустрічаючись з новою задачею, експерт представляє її інакше, ніж новачок. Цей момент добре проілюстровано в дослідженнях вирішення завдань у фізиці. Експерт (скажімо, професор фізики) представляє задачу на мові фізичних принципів, потрібних для її вирішення, наприклад: «ця задача відноситься до типу: будь-яка дія викликає рівну і протилежно спрямована протидія». Новачок (скажімо, студент-фізик першого курсу), навпаки, представляє ту ж саму проблему на мові поверхневих властивостей, наприклад: «це завдання з роду завдань з похилою площиною» (Chi, Glaser & Rees, 1982).
Експерти і новачки розрізняються також використовуваними стратегіями. У дослідженнях рішення фізичних завдань експерти загалом намагаються сформулювати план підходу до задачі, перш ніж виводити рівняння, тоді як новачки, як правило, починають писати рівняння, не маючи в голові загального плану (Larkin et al., 1980).
Експерти вирішують шахову задачу якісно інакше, ніж новачки. Такі експерти, як майстри гри в шахи, зберігають у своїй пам'яті набагато більше специфічних репрезентацій, ніж вони можуть застосувати для розв'язання проблеми.
Ще одна відмінність полягає в тому, що новачки працюють в протилежному напрямку (стратегія руху від мети). Це розходження в напрямку міркування також було виявлено в дослідженнях рішення задач лікарями. Більшість експертів-лікарів міркують в прямому напрямку - від симптому до можливого захворювання, тоді як менш досвідчені колеги міркують у зворотному напрямку - від можливого захворювання до симптому (Patel & Groen, 1986).
Розглянуті характеристики компетентності - множинність репрезентацій; репрезентації, засновані на певних правилах; планування перед дією; рух вперед - це деякі з предметно-орієнтованих процедур, які приходять на зміну слабким методів розв'язання задач, розглянутих раніше.
Вплив мислення на мову
Невже мова ставить нас в рамки якогось особливого світогляду? Згідно найефектнішою формулюванні гіпотези мовного детермінізму (Whorf, 1956), граматика кожної мови являє собою втілення метафізики. Наприклад, тоді як в англійській мові є іменники та дієслова, мова нутка оперує тільки дієсловами, а мова хопі розділяє реальність на дві складові: світ явний і світ неявний. Уорф стверджує, що подібні мовні відмінності формують у носіїв мови образ мислення, незрозумілий для інших. См.→
Як мова може визначати мислення: мовна відносність і мовної детермінізм
Ніхто не сперечається з тезою, що мова та мислення надають один на одного значний вплив. Однак існують розбіжності з приводу твердження, що кожна мова по-своєму впливає на мислення і вчинки говорять на ньому людей. З одного боку, кожен, хто вивчив два і більше мови, дивується тому безлічі особливостей, що відрізняють одну мову від іншої. З іншого боку, ми припускаємо, що способи сприйняття навколишнього світу схожі у всіх людей. См.→