Теорія хаосу
З сайту Gontsjar.ucoz.ru
Фрактали створюються завдяки грі хаосу
Введення в теорію хаосу
Що таке теорія хаосу?
Теорія хаосу це вчення про постійно змінюються складних системах, заснований на математичних концепціях рекурсії, у формі чи рекурсивного процесу або набору диференційних рівнянь, що моделюють фізичну систему.
Неправильні уявлення про теорії хаосу
Широка громадськість звернула увагу на теорію хаосу завдяки таким фільмам, як Парк юрського періоду, і завдяки ним, постійно збільшується побоювання теорії хаосу з боку суспільства. Однак, як і щодо будь-якої речі, висвітлюється засобами масової інформації, щодо теорії хаосу виникло багато неправильних уявлень.
Найбільш часто зустрічається невідповідність полягає в тому, що люди вважають, що теорія хаосу - це теорія про безлад. Ніщо не могло б бути так далеко від істини! Це не заперечення детермінізму і не твердження про те, що впорядковані системи неможливі; це не заперечення експериментальних підтверджень і не заяву про марність складних систем. Хаос в теорії хаосу і є порядок - і навіть не просто порядок, а сутність порядку.
Це правда, що теорія хаосу стверджує, що невеликі зміни можуть спричинити величезні наслідки. Але однією з центральних концепцій в теорії є неможливість точного передбачення стану системи. Загалом, завдання моделювання загальної поведінки системи цілком здійсненна, навіть проста. Таким чином, теорія хаосу зосереджує зусилля не на безладді системи - спадкової непередбачуваності системи - а на успадкованій нею в порядку - загалом у поведінці схожих систем.
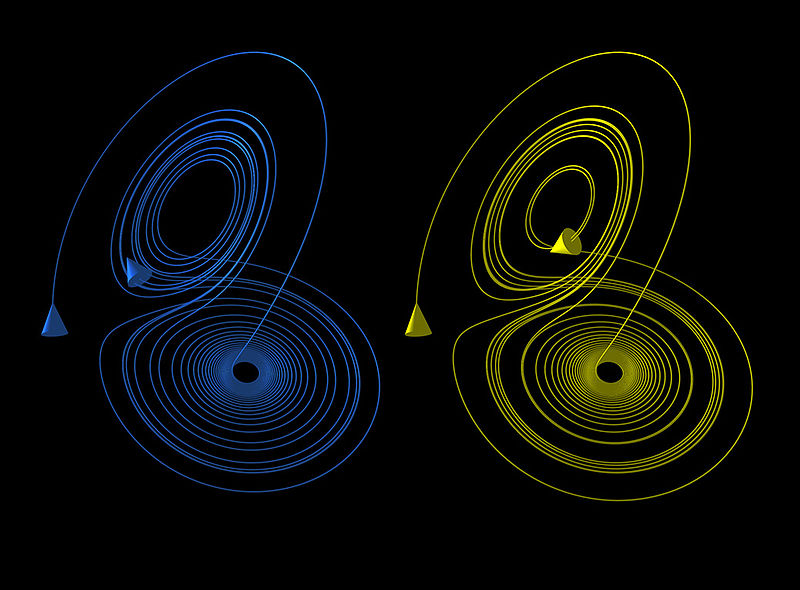
Таким чином, було б неправильним сказати, що теорія хаосу про безлад. Щоб пояснити це на прикладі, візьмемо аттрактор Лоренца. Він заснований на трьох диференціальних рівняннях, трьох константи і трьох початкових умовах.
Теорія хаосу про безлад
Аттрактор представляє поведінку газу у будь-який заданий час, і його стан в певний момент залежить від його стану в моменти часу, що передували даному. Якщо вихідні дані змінити навіть на дуже малі величини, скажімо, ці величини настільки малі, що співмірні з внеском окремих атомів в число Авогадро (що є дуже маленьким числом порівняно зі значеннями порядку 1024), перевірка стану аттрактора покаже абсолютно інші числа. Це відбувається тому, що маленькі відмінності збільшуються в результаті рекурсії.
Однак, незважаючи на це, графік атрактора буде виглядати досить схоже. Обидві системи будуть мати абсолютно різні значення в будь-який заданий момент часу, а графік аттрактора залишиться тим же самим, т. к. він висловлює загальну поведінку системи.
Теорія хаосу каже, що складні нелінійні системи є спадково непередбачуваними, але, в той же час, теорія хаосу стверджує, що спосіб вираження таких непередбачуваних систем виявляється вірним не в точних рівності, а в уявленнях поведінки системи - у графіках дивних атракторів або у фракталах. Таким чином, теорія хаосу, про яку багато думають як про непередбачуваність, виявляється, в той же час, наукою про передбачуваності навіть в найбільш нестабільних системах.
Застосування теорії хаосу в реальному світі
При появі нових теорій, всі хочуть дізнатися, що ж у них хорошого. Отже що хорошого в теорії хаосу? Перше і найважливіше - теорія хаосу - це теорія. А значить, що більша її частина використовується більше як наукова основа, ніж як безпосередньо застосовне знання. Теорія хаосу є дуже гарним засобом поглянути на події, що відбуваються в світі відмінно від більш традиційного чітко детерміністичного погляду, який домінував у науці з часів Ньютона. Глядачі, які подивилися Парк Юрського періоду, без сумніву бояться, що теорія хаосу може дуже сильно вплинути на людське сприйняття світу, і, в дійсності, теорія хаосу корисна як засіб інтерпретації наукових даних по-новому. Замість традиційних X-Y графіків, вчені тепер можуть інтерпретувати фазово-просторові діаграми які - замість того, щоб описувати точне положення якої-небудь змінної в певний момент часу - представляють загальну поведінку системи. Замість того, щоб дивитися на точні рівності, засновані на статистичних даних, тепер ми можемо поглянути на динамічні системи з поведінкою схожим по своїй природі статичні дані, тобто системи з схожими аттракторами. Теорія хаосу забезпечує міцний каркас для розвитку наукових знань.
Однак, згідно сказаного не випливає, що теорія хаосу не має додатків в реальному житті.
Техніки теорії хаосу використовувалися для моделювання біологічних систем, які, безперечно, є одними з найбільш хаотичних систем з усіх що можна собі уявити. Системи динамічних рівностей використовувалися для моделювання всього - від росту популяцій та епідемій до аритмічних серцебиття.
Насправді, майже будь-яка хаотична система може бути змодельована - ринок цінних паперів породжує криві, які можна легко аналізувати за допомогою дивних атракторів на відміну від точних співвідношень; процес падіння крапель протікає з водопровідного крана здається випадковим при аналізі неозброєним вухом, але якщо його зобразити як дивний атрактор, відкривається приголомшливий порядок, якого не можна було б очікувати від традиційних засобів.
Фрактали знаходяться скрізь, найбільш помітні в графічних програмах, як, наприклад, дуже успішна серія продуктів Fractal Design Painter. Техніки фрактального стиснення даних все ще розробляються, але обіцяють вражаючі результати як наприклад коефіцієнта стиснення 600:1. Індустрія спеціальних ефектів в кіно, мала б набагато менш реалістичні елементи ландшафту (хмари, скелі і тіні) без технології фрактальної графіки.
У фізиці фрактали природним чином виникають при моделюванні нелінійних процесів, таких, як турбулентний плин рідини, складні процеси дифузії-адсорбції, полум'я, хмари і т. п. Фрактали використовуються при моделюванні пористих матеріалів, наприклад, в нафтохімії. В біології вони застосовуються для моделювання популяцій і для опису систем внутрішніх органів (система кровоносних судин).
І, звичайно, теорія хаосу дає людям дивно цікавий спосіб того, як придбати інтерес до математики, однією з найбільш мало-популярної області пізнання на сьогоднішній день.