Найкращий IQ-тест

Автор В. А. Васильєв

Весь світ кудись глобалізується, і ми повинні глобализоваться туди ж, і відхилення хоча б в деталях (і навіть швидше в деталях і формою, ніж зміст) сприймається як небезпечне вільнодумство; навпаки, точне дотримання подробиць вкрай вітається нашими партнерами з Першого Світу і навіть служить часом індульгенцією для невідповідності по суті.

Тому визнання і авторитет у Першому Світі - аргумент, який діє майже безвідмовно. На розсудливі доводи вам заперечать: "А от у розвинених країнах...", і продовжувати спір буде так само непристойно, як оскаржувати Святе Письмо. Про одному з таких авторитетів я і збираюся поговорити у зв'язку з наукою тестологией, що грає все більшу роль у нашому житті.

І так, у розвинених країнах" при наймі на роботу (і для інших призначень) досить часто використовується система тестів, на підставі яких випробуваним присвоюється числовий показник, іменований IQ (що його винахідники розшифровують як Intelligence Quotient - коефіцієнт інтелекту).

При стандартних випробуваннях на IQ пропонується за певний термін (зазвичай 30 або 90 хвилин) відповісти на сорок питань.

Приклади таких комплектів завдань подано в книжці [1], написаній Р. Айзенком (Hans Eysenck) - як сказано в анотації, "класиком сучасної психології" і "самим знаменитим дослідником IQ". Правда, сам він у вступі до книги демонструє зразкову скромність, звинувачуючи журналістську братію в абсолютному незнанні (utter ignorance), що складається в тому, що вони, мовляв, несправедливо проголошують його винахідником IQ і людиною, що довели спадковий характер IQ; проте не викликає сумнівів, що саме йому ці тести зобов'язані своєю популярністю, усталеною структурою і набором типів завдань.

Ймовірно, у зв'язку з тим, що поняття інтелекту традиційно включається здатність до логічного мислення і наявність просторової уяви, в кожному з восьми тестів, наведених в [1], міститься по дві "логічні" і дві "геометричні" завдання. Їх я і хочу прокоментувати.

Логіка

У всіх шістнадцяти логічних завданнях в якості умови дається кілька тверджень про наявність спільних елементів у деяких досить екзотично визначаються множин або про те, що одна з цих множин є частиною іншого. Потім заявляється, що ще одне твердження такого типу є наслідком наведених умов; випробуваний повинен відповісти на питання, чи вірно останнє висловлювання.

Варіант 1. завдання 11

Деякі трактори - глечики; а у більшості глечиків помаранчеві носи; всі ті, у кого носи помаранчеві, крякають; таким чином, деякі з тих, хто крякає, - трактори^[1].

Не слід лякатися цих дивних заяв: по суті, це стандартна завдання на алгебру і логіку теорії множин. Просто замість нудних літер A, B, C і т. д. для позначення якихось абстрактних множин використовуються інші імена - трактори, глечики, "ті, хто крякає" і т. п. Висловлювання "деякі трактори - глечики" означає, що відповідні множини перетинаються (тобто існують об'єкти, що входять і в той безліч, і інше);вислів "всі кораблі - пінгвіни" означає, що перше безліч - частина другого. Вислів "всі телефони бояться книжкових шаф", ймовірно, слід розуміти як відсутність у двох множин загальних елементів (хоча "класику сучасної психології" слід би знати, що боязнь собі подібних - явище лише ненормальне, але не неможливе). Тому ці формулювання зовсім не страшні. Страшно інше.

Авторський відповідь на дану задачу: останнє висловлювання істинно.

Цей відповідь невірний: на діаграмі показана ситуація, в якій всі умови виконані, а висновок - немає. (Далі на всіх діаграмах безлічі схематично зображені іменованими прямокутниками; ім'я кожного прямокутника повністю в ньому міститься.)

Варіант 1. завдання 25

​Всі кораблі - пінгвіни, а у всіх пінгвінів на ногах ростуть газонокосарки; крім того, деякі пінгвіни їдять холодильники; і всі фени їдять холодильники. Але ніхто з тих, у кого на ногах ростуть газонокосарки, не є феном; так що жоден корабель не їсть холодильники^[2].

Авторський відповідь і пояснення: помилково. Деякі кораблі їдять холодильники.

Хоча відповідь вірний, обґрунтування помилково. Насправді завідомо неправдивим при даних умовах не є вислів "жоден корабель не їсть холодильники" (на підставі умов достовірне твердження про його істинності чи хибності зробити неможливо), а твердження (виражене словами "отже") про те, що це висловлювання випливає з умов. На діаграмі показана схема перетину множин, що суперечить авторському твердженням: вона задовольняє всім цим завдання, але в неї жоден корабель не їсть холодильники.

Варіант 2 завдання 14

Деякі гобліни - сніжинки; деякі сніжинки добре грають у баскетбол; у всіх, хто добре грає в баскетбол, по три голови; отже, всі ті, у кого по три голови, - гобліни^[3].

Авторський відповідь: істинно.

Цей відповідь невірний. Більш того, можливий варіант, коли ніхто з тих, у кого по три голови, не є гобліном (див. діаграму).

Варіант 3 завдання 11

Вирішена автором правильно. Тому я не наважуюсь порушити авторське право і опублікувати умова цієї задачі. З іншого боку, я сподіваюся, що несанкціонована публікація неправильних завдань не завдає такої великої шкоди інтелектуальної власності, щоб прийти в суперечність із законом. (Те ж відноситься до іншим чотирьом вірним завдань: №№ 3 і 26 варіанта 4 і №№ 11 і 23 варіанта 8.)

Варіант 5 завдання 13

Всі ящики - гітари; всі гітари - хороші борці. У деяких хороших борців перетинчасті лапи; отже, у деяких ящиків перетинчасті лапи^[4].

Авторський відповідь: вірно.

Цей висновок хибний, як показує діаграма.

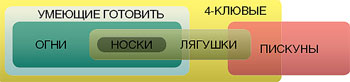
Варіант 5 завдання 29

Всі шкарпетки - жаби, і у всіх жаб по чотири дзьоба; всі вогні вміють готувати їжу, а у всіх, хто вміє готувати їжу, по чотири дзьоба; деякі жаби вміють пищати. Всі шкарпетки - вогні, отже, деякі вогні пищать^[5].

Авторський відповідь: вірно.

Цей висновок є помилковим, як показує діаграма.

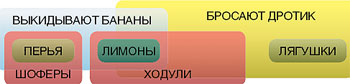
Варіант 6 завдання 22

Всі пір'я - шофери і завжди викидають банани з вікна. Жаби іноді можуть кинути дротик на три милі, як і деякі лимони. Лимони - ходулі і завжди викидають банани з вікна. Отже, і пір'я, і ходулі завжди викидають банани з вікна^[6].

Авторський відповідь: істинно.

Цей відповідь невірний. Неможливо зробити висновок, що всі ходулі задовольняють якомусь умові, не маючи жодної умови, також відноситься до всіх ходулям (а не до їх частини, що складається з лимонів). Точніше, таке твердження можна зробити тільки в тому випадку, коли сукупність вступної інформації внутрішньо суперечлива; як показує діаграма, в даному випадку це не так.

Варіант 7 завдання 12

Всі кукурудзяні пластівці - коні. Всі кукурудзяні пластівці носять червоні гудзики і іноді грають в бінго. Пшеничні коржі іноді грають в бінго. Алмази - пшеничні коржі, отже, алмази і коні іноді грають в бінго^[7].

Умову задачі можна розуміти трьома різними способами (що саме по собі є істотним недоліком), так як вислів "алмази і коні іноді грають в бінго" допускає три різні інтерпретації. У всіх трьох випадках авторський відповідь є помилковим.

Перше розуміння: кожен алмаз і кожна кінь іноді грає в бінго. У цьому випадку авторський відповідь є помилковим з тієї ж причини, що і в попередній задачі: неможливо зробити достовірне твердження про всіх конях, маючи інформацію лише про тих з них, які одночасно є кукурудзяними пластівцями (див. діаграму).

Друге розуміння: бувають моменти часу, коли якісь алмази і якісь коні грають в бінго. В цьому випадку відповідь очевидно неправильний, тому що ніде в умові нічого не сказано про те, хто з ким грає одночасно.

Нарешті, третє розуміння: бувають моменти, коли якісь алмази грають в бінго, і бувають (можливо, інші) моменти, коли якісь коні грають в бінго. Але тоді в такому ж сенсі треба розуміти умову "пшеничні коржі іноді грають в бінго": бувають моменти, коли якісь коржики грають в бінго. При цьому не виключено, що це трапляється тільки з тими коржами, які не є алмазами, отже, авторський відповідь знову невірний.

Варіант 7 завдання 40

Деякі листівки - білі ведмеді, а деякі мийні машини часто чхають; крім того, дикобрази говорять по-китайськи, а всі ті, хто говорить по-китайськи, часто чхають. Але жоден білий ведмідь часто не чхає. Деякі мийні машини говорять покитайски, а всі листівки - мийні машини. Отже, деякі листівки говорять по-китайськи^[8].

Авторський відповідь: істинно.

Це висновок помилково чинності наступного прикладу. Припустимо, що а) безлічі листівок і білих ведмедів збігаються між собою, б) безлічі дикобразів, чихателей і знавців китайської мови теж збігаються між собою, в) безліч мийних машин є об'єднанням множин а) і б), причому два останніх множини не мають спільних елементів. Тоді всі умови завдання виконані, а висновок - немає.

Настільки ж невірно вирішені завдання 2:39, 3:26 і 6:11. Отже, автор правильно вирішив не більше п'яти з шістнадцяти своїх власних логічних завдань, і ще в трьох дав правильну відповідь на підставі неправильного міркування.

Відповідно до таблиці, наведеної в [1] на стор 207, такий відсоток правильних рішень (5/16 = 12,5/40) дає значення IQ, рівну приблизно 106. Відповідно до роз'яснення на 14 стор. в [2], це дещо ближче до рівня кваліфікованих працівників (109 балів), ніж слабо кваліфікованих (98 балів); втім, оскільки вище "кваліфікованих працівників" там вказані ще три ступені розвитку, у тому числі "висококваліфіковані, канцелярські працівники" (117 балів), до посади клерка людини з таким показником підпускати не можна. З іншого боку, серед сорока завдань (з яких треба набрати дванадцять з половиною) деякі вимагають вибору відповіді - так і ті, як правило, не з двох, а з шести варіантів. У той же час в логічних завданнях достатньо лише вгадати один відповідь з двох. Для того щоб в середньому дати вісім правильних відповідей на шістнадцять питань типу так/немає, можна взагалі ні про що не думати, а довільно розставляти відповіді.